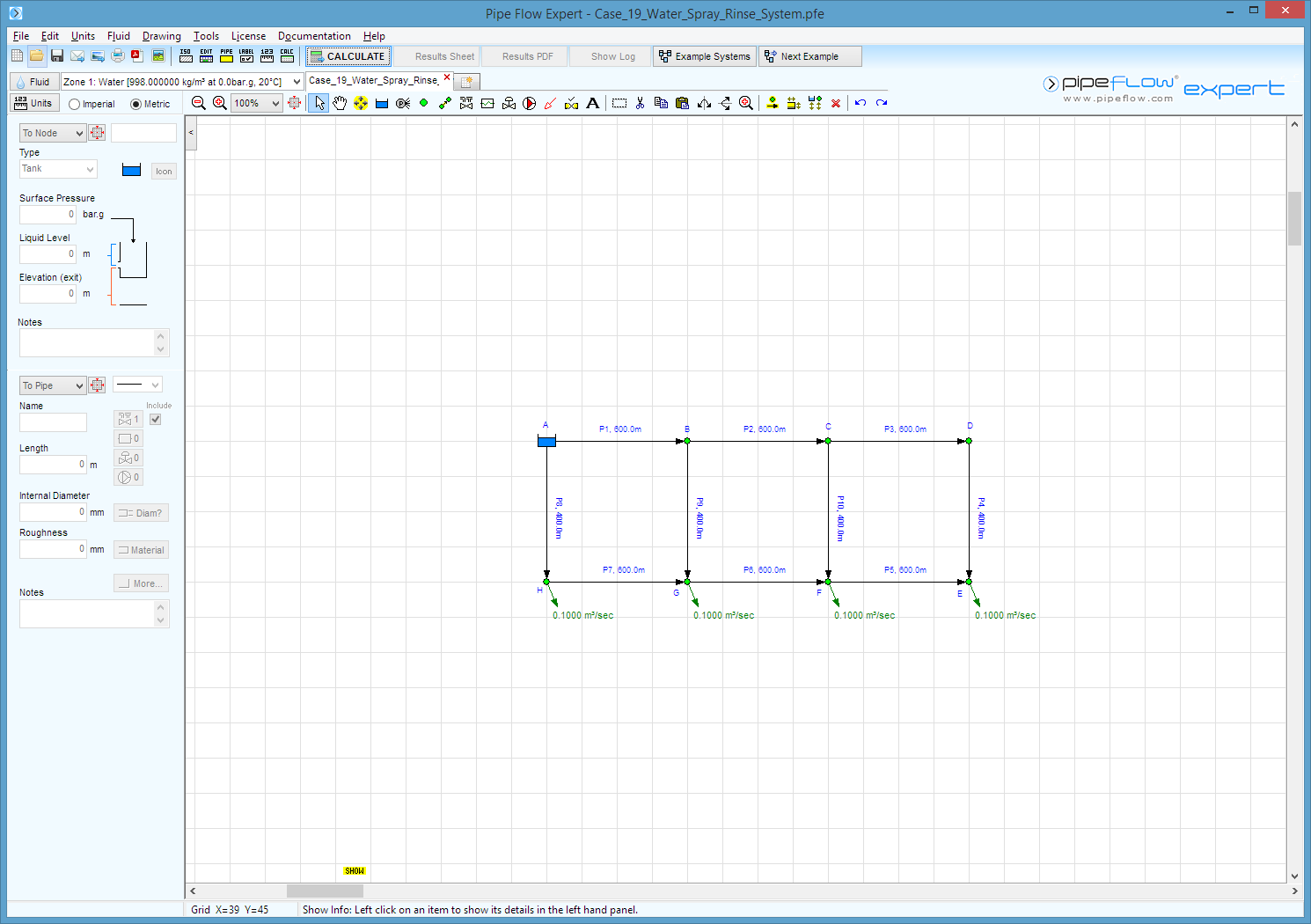
Case 19: Water - Spray Rinse System
Reference: 2500 Solved Problems in Fluid Mechanics and Hydraulics, 1989, McGraw-Hill, Jack B. Evett, Ph. D., Cheng Liu, M.S., Page 322, Example problem 13.5
Pipe Flow Expert File: Case_19_Water_Spray_Rinse_System.pfe
Problem Description:
Water is pumped from a single source around a spray rinse pipe network.
Out flow demands are specified at 4 points of the network.
The published text is based on a solution using the empirical Hazen-Williams equation to calculate friction head losses.
Assume C = 120 for all pipes.
The published results are based on the Hardy Cross method which has been used to balance the flow around the loops.
Calculate the flow rate each individual pipe.
Fluid Data: Water at 20° C (assumed).
Result Comparison:
|
Data Item |
Published data |
Pipe Flow Expert |
|
AB Flow rate (m³/s) |
0.215 |
0.2182 |
|
BG Flow rate (m³/s) |
0.095 |
0.0962 |
|
GH Flow rate (m³/s |
0.085 |
0.0818 |
|
HA Flow rate (m³/s |
0.185 |
0.1818 |
|
BC Flow rate (m³/s |
0.120 |
0.1219 |
|
CF Flow rate (m³/s |
0.064 |
0.0646 |
|
FG Flow rate (m³/s |
0.080 |
0.0781 |
|
GB Flow rate (m³/s) |
0.095 |
0.0962 |
|
CD Flow rate (m³/s) |
0.056 |
0.0574 |
|
DE Flow rate (m³/s) |
0.056 |
0.0574 |
|
EF Flow rate (m³/s) |
0.044 |
0.0426 |
|
FC Flow rate (m³/s) |
0.064 |
0.0646 |
Commentary:
The published data and the calculated results compare well.
The Pipe Flow Expert results have been rounded to 3 decimal places for comparison purposes.
The Pipe Flow Expert results have been based on calculations using the Darcy-Weisbach equation, which provides more accurate results than those obtained by using the Hazen Williams equation.

