Case 18: Elevated Pipeline Inlet Pressure
Reference: Gas Pipeline Hydraulics, 2005, CRC Press, E. Shashi Menon, Chapter 3, page 87 Example 1
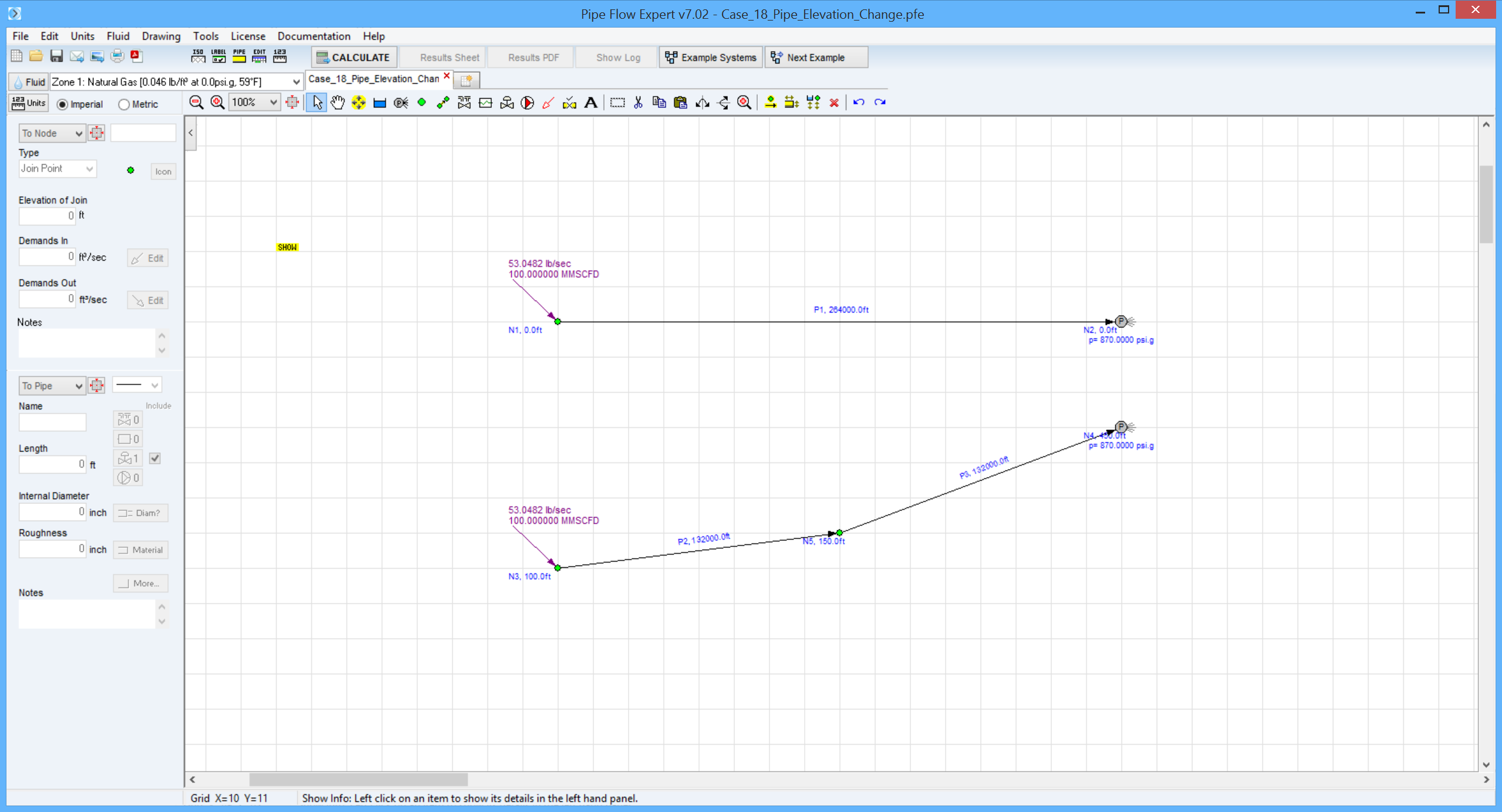
Pipe Flow Expert File: Case_18_Pipe_Elevation_Change.pfe
Problem Description:
A gas pipeline, 15.5 inch internal diameter, 50 miles long, transports natural gas (SG = 0.6 and viscosity = 0.0119 centipoise) at a flow rate of 100 MMSCFD at an inlet temperature of 60 °F.
Assuming isothermal flow, calculate the inlet pressure required if the required delivery pressure at the pipeline terminus is 870 psi.g.
Case A: No elevation change along the pipeline length.
Case B: Elevation changes as follows: inlet elevation of 100 ft, delivery point elevation of 450 ft, with midpoint elevation of 250 ft.
The calculation method used for the published data was the General Flow equation.
Fluid Data: Natural Gas with specific gravity 0.6, 60 °F, 14.696 psi.g (0.04582 lb/ft3), viscosity 0.01191 centipoise.
Pipe Data: Absolute roughness 0.0007 inches.
Calculation Method: General Isothermal Flow equation, Node Adjust Method.
Standard Atmospheric Model: 60 °F, 14.696 psi
Gas Physical Model: Real Gas Model (Ideal Gas Law with CNGA-calculated compressibility factor).
Result Comparison:
|
Data Item |
Published data |
Pipe Flow Expert |
|
Inlet pressure (psi.g) for Case A |
985.66 |
985.62 |
|
Inlet pressure (psi.g) for Case B |
993.64 |
992.78 |
Commentary:
The published data and the calculated results compare well.
The published data was calculated using a compressibility factor of 0.8666, which was derived using the CNGA formula as applied to the first arrangement of the system.
For simplification the published data then used the same compressibility factor for each pipe in the second arrangement of the system.
Pipe Flow Expert calculated an independent compressibility factor for each pipe (0.8662, 0.8617, 0.8693) using the CNGA formula.

