Reference: 2500 Solved Problems in Fluid Mechanics and Hydraulics, 1989, McGraw-Hill, Jack B. Evett, Ph. D., Cheng Liu, M.S., Page 483, Example problem 16.78


Pipe Flow Expert File: Case_41_Carbon_Dioxide_Flow_Through_A_Pipe.pfe


Problem Description:

Carbon Dioxide at temperature of 100°F flows through a pipe with 6” internal diameter.

The pipe internal roughness is 0.002 ft (0.024”). 

The flow is isothermal. 

The pressure at the start of a 120 ft long horizontal pipe section is 160 psig the pressure at the end of the section is 150 psig.

Calculate the weight flow rate of the air.

 

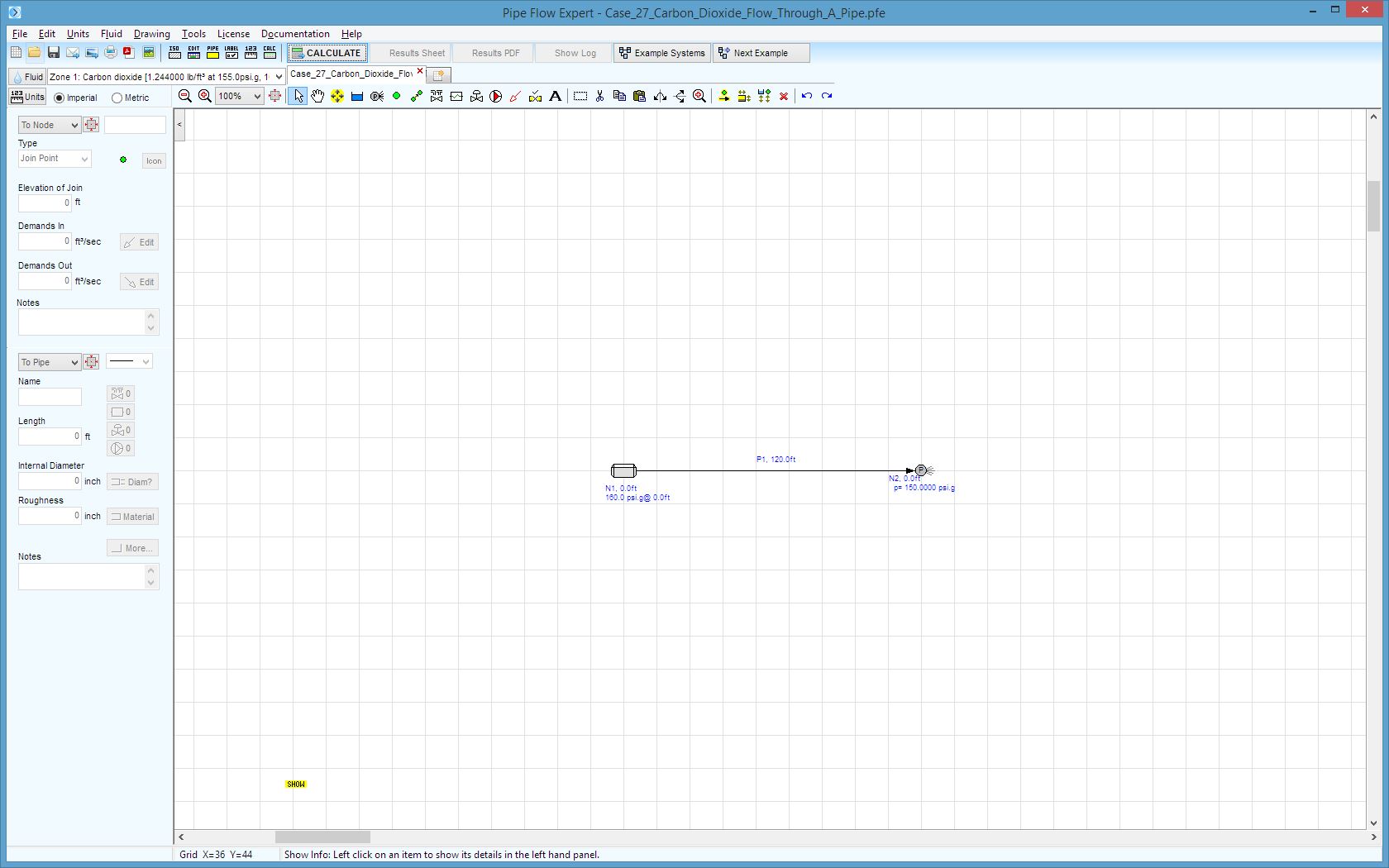
A screenshot of a computer??Description automatically generated


Fluid Data: Carbon Dioxide at 155 psi gauge and 100°F, density 1.244000 lb/ft3, viscosity 0.015500 centipoise.

       Pipe Flow Expert will automatically calculate for compression of the gas. The fluid could have been

       defined at any pressure, although here it was defined at the average pressure condition of 155 psi.g.

       The fluid data must however be defined at the required temperature.

Pipe Data: Internal diameters of 6 inches. Roughness 0.0024 inches.

Calculation Method: General Isothermal Flow equation, Node Adjust Method.

Standard Atmospheric Model: 68 °F, 14.696 psi absolute

Gas Physical Model: Ideal Gas Law


Result Comparison: 


Data Item

Published data

Pipe Flow Expert

Weight of Flow (lb/sec)

  25.3 

   25.5278

Reynolds Number

5000000

6241277

Friction Factor

0.0285

0.0284


Commentary: 

The published data and the calculated results compare well.

The published text assumes an initial Reynolds Number greater than 1000000 and a friction factor of 0.0285 which is used to estimate the weight of flow as 25.3 lb/sec. 

The weight of flow is then used to recalculate the Reynolds Number as 5000000. 

The new Reynolds Number is greater than the initial assumption of the Reynolds Number and is taken as confirmation of the previously calculated weight of flow.


The Pipe Flow Expert program uses the Colebrook-White equation to determine friction factors that are used in the General Isothermal Flow equation. 

The Colebrook-White equation is usually considered to be more accurate than a value read from a Moody Chart.